Bias – Variance Trade-off
Bias-variance trade-off is one of the most important concepts that anyone in machine/deep learning should know. It is a way of understanding over-fitting and under-fitting. Errors in your model can be either reducible or non-reducible. Knowledge about these components allows you to take better decisions about your model selection and training.
The general task in machine learning is the estimation of the underlying function.
In estimation theory, for searching optimal estimators an optimal criterion is generally adopted. Mean squared error is the natural one and is defined as follows.
This measures the average mean squared deviation of the estimator from the true value. This error can be decomposed into two terms namely bias and variance. The derivation is given below.
The bias variance decomposition can be represented with following triangle relation.
Bias is the difference between the expected value of the estimator and the actual underlying function. Variance is the variability of the model. In estimation theory, different types of estimators exist. However, from a practical point of view minimum MSE estimators need to be abandoned because this criterion leads to unrealizable estimators. We often turn to Minimum Variance Unbiased (MVU) Estimators which have further specialized versions such as Best Linear Unbiased Estimators (BLUE) etc.
In the case of deep learning, the networks work as powerful estimators without having any explicit definition. All the analysis done above is directly application in this case too.
The observations Y that are available to us always contain some inherent noise. It can be written as follows:
This assumption adds one term into the MSE decomposition. Since the derivation is almost same as without the noise term, I’m writing the end equation directly.
Bayes error refers to the lowest possible error for any classifier and is analogous to irreducible error. It is also known as the optimal error. Even if you build a perfect model, this error cannot be eliminated. This is because the training data itself is not perfect and contains noise.
So, the total error for your model is the addition of three kinds of error namely error due to bias in the model, error due to the model variance and finally irreducible error.
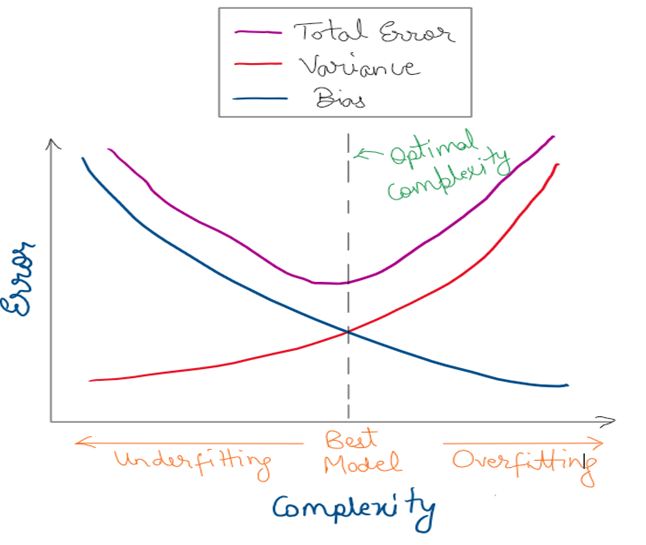
This relation can be explained by the following graph.
As the complexity of your model increases the bias goes on decreasing and the variance goes on increasing. The total error goes on increasing until the optimal complexity point. This is where just Bayes Error is left and the model has maximum performance.
Following are few examples of how under-fitting, optimal-fitting and over-fitting looks like.
For models having high variance, the underlying noise is also captured. For models having high bias, the model isn’t able to capture the underlying pattern in the data. Optimal model is the best model and is the most generalizable.
That wraps up the discussion about the bias-variance trade-off. In the next post, I’ll be talking about how to handle the cases of high bias and high variance, in other words, under-fitting and over-fitting. Thank you for reading and hope you liked the post!














