Explain about Eigen values and Eigen Vectors?
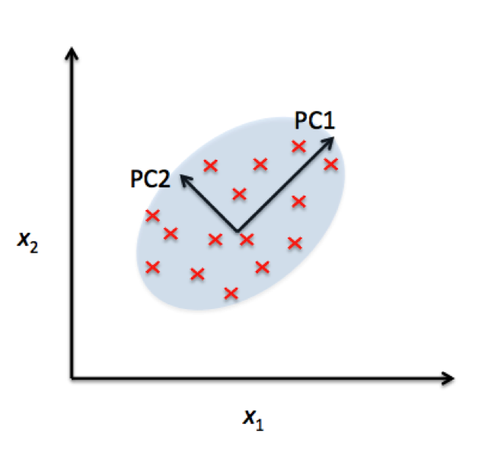
Eigenvector —Every vector (list of numbers) has a direction when it is plotted on an XY chart. Eigenvectors are those vectors when a linear transformation (such as multiplying it to a scalar) is performed on them then their direction does not change. This attribute of Eigenvectors makes them very valuable as I will explain in this article.
Eigenvalue— The scalar that is used to transform (stretch) an Eigenvector.
Eigenvectors and eigenvalues are used to reduce noise in data. They can help us improve efficiency in computationally intensive tasks. They also eliminate features that have a strong correlation between them and also help in reducing over-fitting.
Eigenvalues and Eigenvectors have their importance in linear differential equations where you want to find a rate of change or when you want to maintain relationships between two variables.
We can represent a large set of information in a matrix. One eigenvalue and eigenvector is used to capture key information that is stored in a large matrix. Performing computations on a large matrix is a very slow process. To elaborate, one of the key methodologies to improve efficiency in computationally intensive tasks is to reduce the dimensions after ensuring most of the key information is maintained.
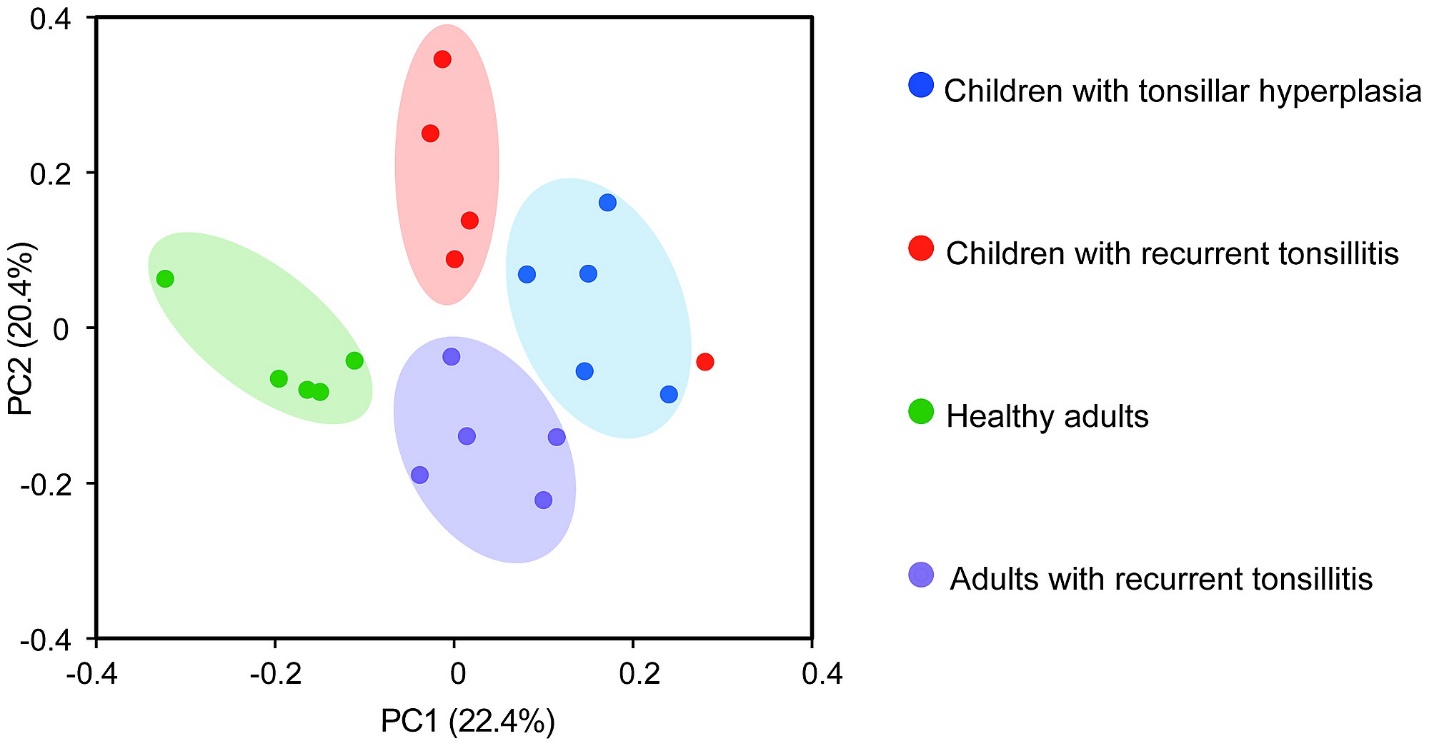
A component analysis is one of the key strategies that is utilized to reduce dimension space without losing valuable information. The core of component analysis (PCA) is built on the concept of eigenvalues and eigenvectors.
Eigenvectors and Eigenvalues are used in facial recognition techniques such as Eigen Faces. They are used to reduce dimension space. At times, this can increase your dimension space to 100+ columns.
The technique of Eigenvectors and Eigenvalues are used to compress the data. Algorithms such as PCA rely on eigenvalues and eigenvectors to reduce the dimensions.
Eigenvectors and Eigenvalues can be used to construct spectral clustering. We can also use eigenvector to rank items in a dataset.
Eigenvectors are used to make linear transformation understandable. Eigenvectors stretches/compresses an X-Y line chart without changing its direction.